
トップ100中学一年 数学 正負の数 最高のぬりえ
最大公約数まとめ ①最大公約数とは、 公約数の中で一番大きな数 のこと。 「2つ以上の正の整数に共通する約数の中で一番大きい数」を指す ②約数は、必ず「元の数と同じか、それよりも小さな数」になる。 24 の約数は必ず 24 以下であり、 36 の約数は反対の性質の表し方 反対の性質をもつ量は、正の数と負の数を使って表すことができます。 このように、正の数で表している量を負の数で表すためには反対の言葉を用います。 いくつか例題を見ながら確認しておきましょう。 例題 現在から 分後
正の数負の数 練習問題
正の数負の数 練習問題-この直した式の中で加法の記号 + で結ばれた数,すなわち, 2,4,5,11 をこの式の「項」といいます。 加法の+とカッコを消して, 項だけをそのまま書き出します。 式の初めの項が正の項のときは, 符号+を省く約束があります。正の数や負の数のデータが1列に大量にあるような場合は、関数を使用する方が楽で確実です。この場合も「1」を乗算して正の数にしています。 空いた列を利用して、次の式を設定します。 =IF(A1<0,A1*1,A1) 式を確定後、最後の行まで数式をコピーします。

正負の数 の足し算 引き算 計算ドリル 問題集 数学fun
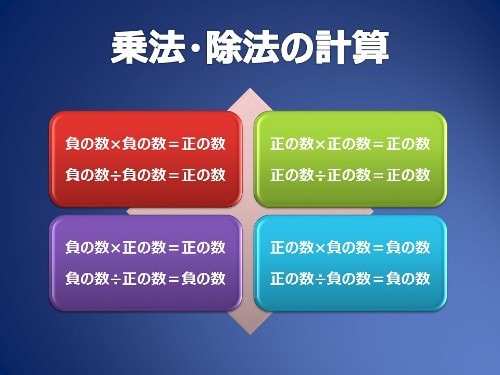
隣り合う数の間に2数の和を書いていくクレペリン検査と同じような内容です。( )のない正負の数の和の計算にはぴったりです。 俵算 加法 解答が書いてあります。生徒は自分で正誤が分かります! 完全正解する時間を記録させます!正負の数の利用 (正負の判定) 正の数 正の数 = 正の数 負の数 負の数 = 負の数 異符号の積は負の数、 同符号の積は正の数 (1) a, b がともに正の数のとき、常に成り立つのはどれか。 すべて答えよ。 ab>0 ab0 ab √3=(自然数ではない、正の実数) √4=2(自然数) というように、ルートの中身が二乗の数になっていればルートが外れて自然数であることが分かります。 ルートの中身12nを素因数分解すると、 となります。 nは自然数なので、1から順番に自然数を代入
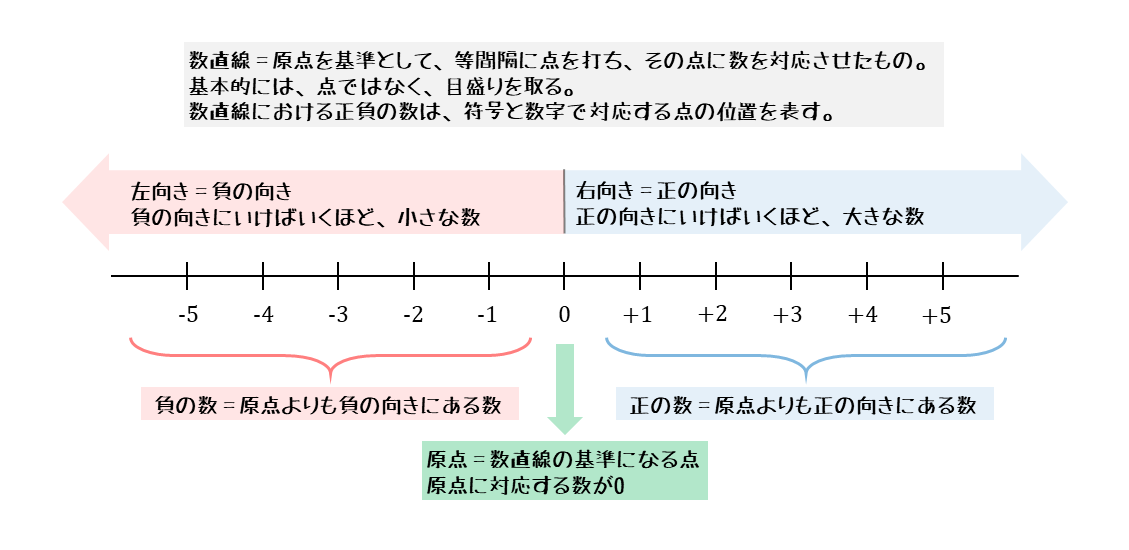
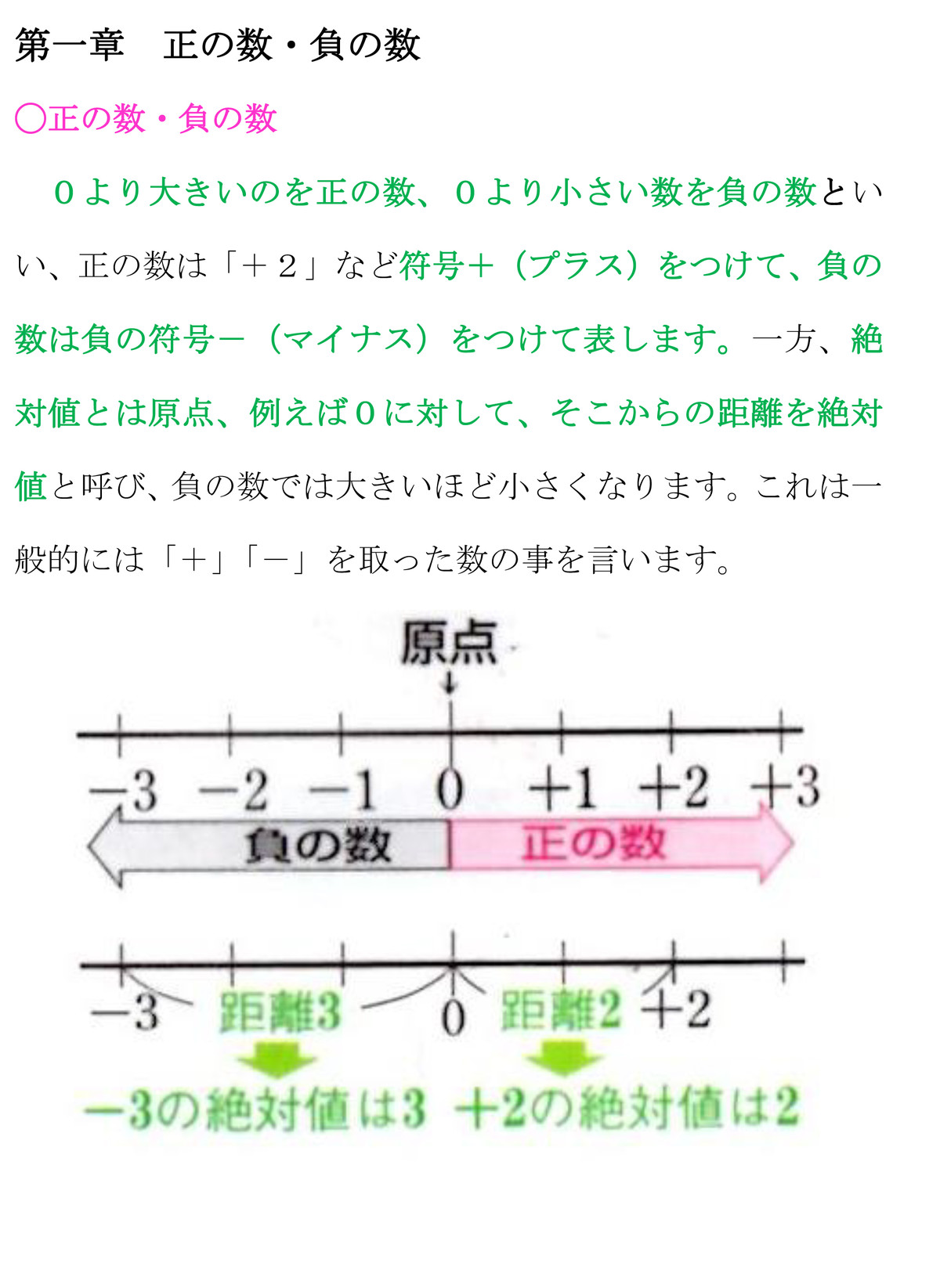
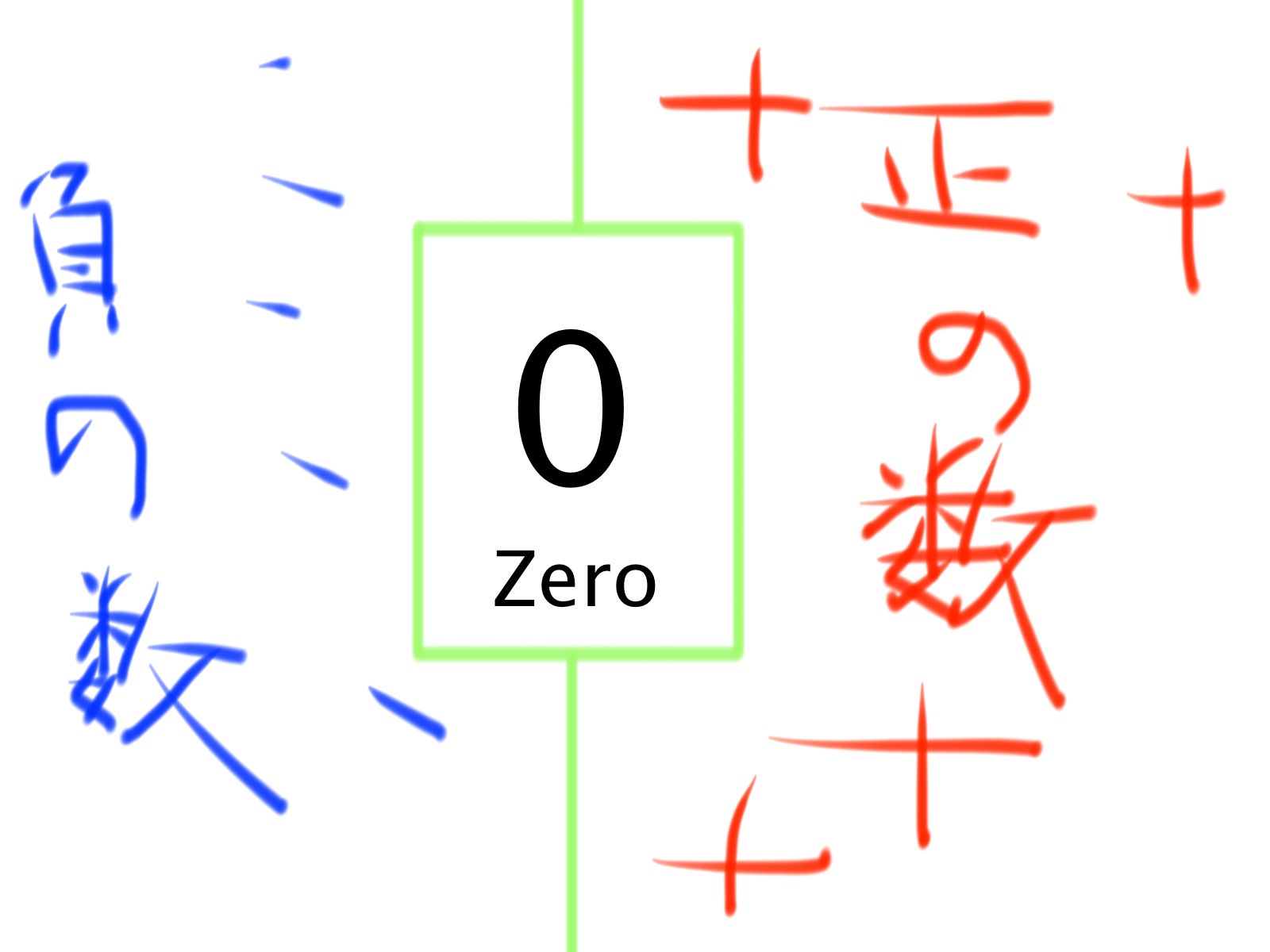
底 \(a\) が正の数ならば、何乗しても(\(y\) がどんな値をとっても)真数 \(x\) は常に正の値をとります。 実際にグラフを見ると一目瞭然です。 以上が、真数条件・底の条件が存在する理由正の有理数全体の集合 Q \mathbb{Q}_ Q と N \mathbb{N} N の濃度が等しいことを言えばよい。 正の有理数 q p \dfrac{q}{p} p q を p q pq p q を小さい順に並べて既約分数のみ残して番号を振っていけば, Q \mathbb{Q}_ Q から N \mathbb{N} N への全単射が構成できる:数直線と絶対値 数直線 小学校で用いていた数直線を0から左の方に伸ばし0より小さい数を表せるようにする。 0 1 2 3123 原点 大 小 正の数・負の数を考えるときには数直線を使い、慣れるまでは数直線を書いて考える。 慣れてきたら頭の中に数直線を思い浮かべて考えるようにする。
正の数負の数 練習問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
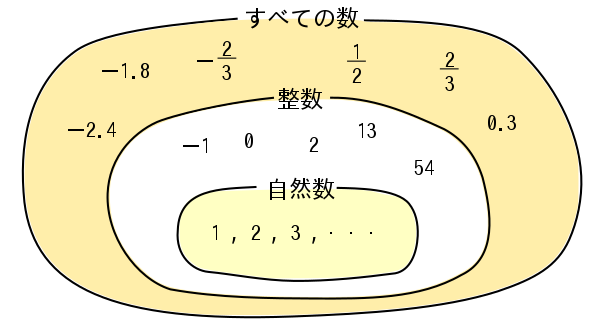 |  | |
 |  |  |
 |  | |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
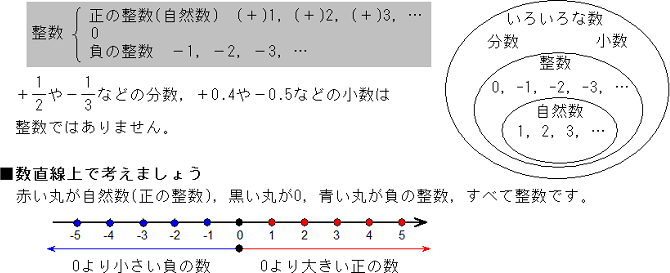 | 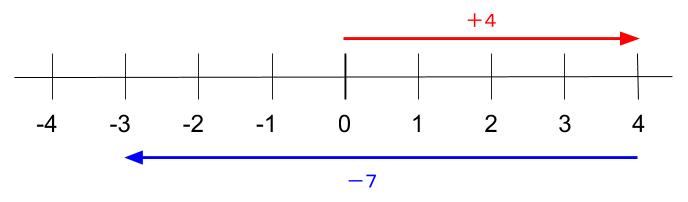 | 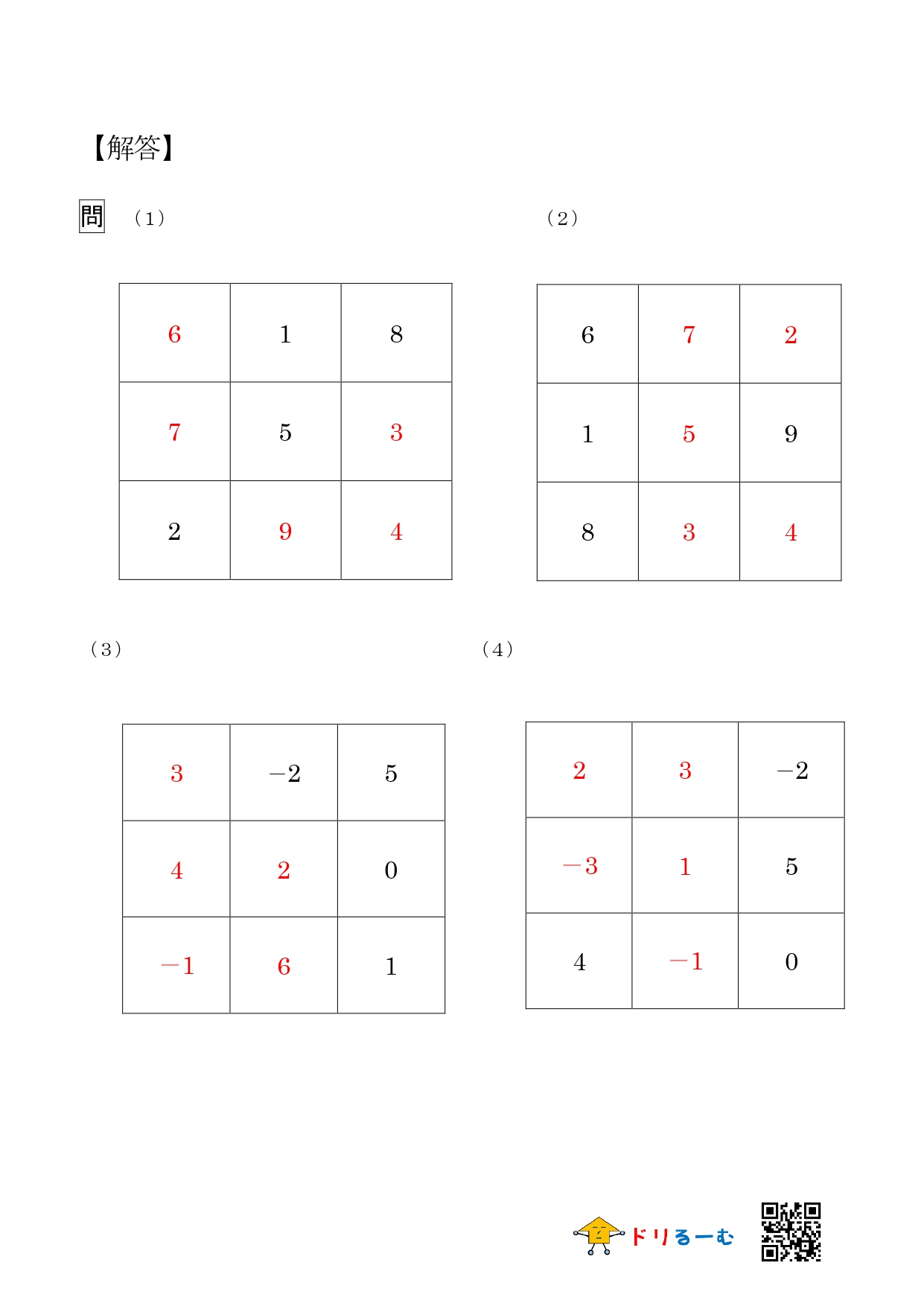 |
 |  | |
 |  | |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | %E3%82%92%E5%A4%96%E3%81%99%E2%97%8F.png) |
 |  |  |
 |  | |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 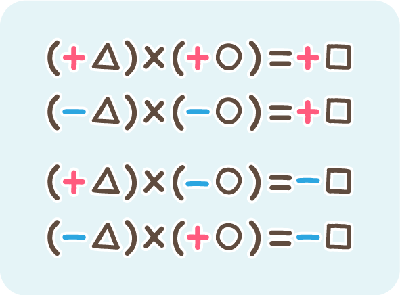 |  |
 | ||
「正の数負の数 練習問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
次に,正の数・負の数の判定についてです。これは,与えられた条件から, ある数の符号が正であるのか,負であるのかを判定する問題です。これだけ 聞くと,「どんな問題だろう? 難しそうだな」と思うかもしれませんが,こ 正十二面体と正二十面体: 辺の数が同じ、面の数と頂点の数が互いに逆になっている。 辺の数・頂点の数 公式一覧 正四面体(面の形は正三角形) 辺の数 3(辺)×4(面)÷2=6 頂点の数 3(点)×4(面)÷3(1頂点を共有する面)=4
Incoming Term: 正の数負の数 計算問題 プリント, 正の数負の数 練習問題, 正の数負の数 教え方, 正の数 負の数 プリント, 正の数負の数, 正の数負の数 発展問題, 正の数負の数 文章問題 応用問題, 正の数負の数 トランプ,




0 件のコメント:
コメントを投稿